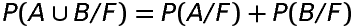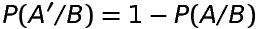If A and B are two envents associated with a random experiment, then the probability of occurence of the event A under the condition that B has occurred and P(B)≠0
Thus P(A/B)=probability of occurence of event A given that event B has already occured and P(B)≠0
Let S be the sample space having ‘n’ equal likely outcomes of a random experiment. Let A and B be two events of sample space S.
a is number of outcomes in A b is number of outcomes in B t is number of outcomes in A∩B
Then
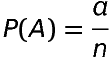
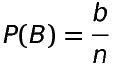
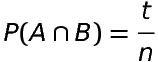
Note: The outcomes of B which are favourable to A are the common outcomes of A and B that is, outcomes of A&capB
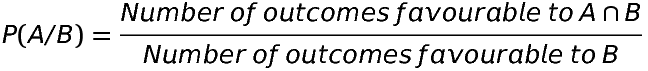
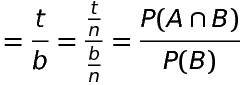provided P(B)≠0
or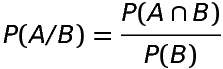
provided P(B)≠0
Similarly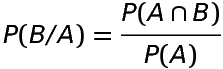
provided P(A)≠0
Properties of Conditional Probability
The conditional probability of an event A given that B has occurred lies between 0 and 1
If A and B are two events associated with a random experiment having sample space S and if F
is an event such that P(F)≠0, then
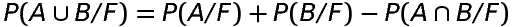and if A and B are disjoint sets
