Permutation : Permutation means arrangement of things. The word arrangement is used, if the order of things is considered.
Combination: Combination means selection of things. The word selection is used, when the order of things has no importance.
Example: Suppose we have to form a number of consisting of three digits using the digits 1,2,3,4, To form this number the digits have to be arranged. Different numbers will get formed depending upon the order in which we arrange the digits. This is an example of Permutation.
Now suppose that we have to make a team of 11 players out of 20 players, This is an example of combination, because the order of players in the team will not result in a change in the team. No matter in which order we list out the players the team will remain the same! For a different team to be formed at least one player will have to be changed.
Now let us look at two fundamental principles of counting:
Addition rule : If an experiment can be performed in ‘n’ ways, & another experiment can be performed in ‘m’ ways then either of the two experiments can be performed in (m+n) ways. This rule can be extended to any finite number of experiments.
Example:
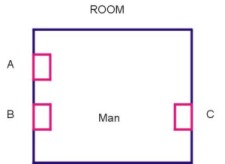
Suppose there are 3 doors in a room, 2 on one side and 1
on other side. A man want to go out from the room.
Obviously he has ‘3’ options for it. He can
come out by door ‘A’ or door ‘B’ or
door ’C’.
Multiplication Rule : If a work can be done in m ways, another work can be done in ‘n’ ways, then both of the operations can be performed in m x n ways. It can be extended to any finite number of operations.
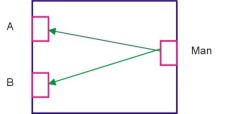
Example.: Suppose a man wants to cross-out a room, which has 2 doors on one side and 1 door on other site. He has 2 x 1 = 2 ways for it.
Factorial n : The product of first ‘n’ natural numbers is denoted by n!.
n! = n(n-1) (n-2) ………………..3.2.1.
Ex. 5! = 5 x 4 x 3 x 2 x 1 =120
Note 0! = 1
Proof n! =n, (n-1)!
Or (n-1)! = [n x (n-1)!]/n = n! /n
Putting n = 1, we have
O! = 1!/1
or 0 = 1
Permutation
Number of permutations of ‘n’ different things taken ‘r’ at a time is given by:-
nPr = n!/(n-r)!
Proof: Say we have ‘n’ different things a1, a2……, an.
Clearly the first place can be filled up in ‘n’ ways. Number of things left after filling-up the first place = n-1
So the second-place can be filled-up in (n-1) ways. Now number of things left after filling-up the first and second places = n – 2
Now the third place can be filled-up in (n-2) ways.
Thus number of ways of filling-up first-place = n
Number of ways of filling-up second-place = n-1
Number of ways of filling-up third-place = n-2
Number of ways of filling-up r-th place = n – (r-1) = n-r+1
By multiplication – rule of counting, total no. of ways of filling up, first, second — rth-place together :-
n (n-1) (n-2) ———— (n-r+1)
Hence:
nPr
= n (n-1)(n-2) ————–(n-r+1)
= [n(n-1)(n-2)———-(n-r+1)] [(n-r)(n-r-1)—–3.2.1.] / [(n-r)(n-r-1)] —-3.2.1
nPr = n!/(n-r)!
Number of permutations of ‘n’ different things taken all at a time is given by:-
nPn = n!
Proof
:
Now we have ‘n’ objects, and n-places.
Number of ways of filling-up first-place = n
Number of ways of filling-up second-place = n-1
Number of ways of filling-up third-place = n-2
Number of ways of filling-up r-th place, i.e. last place =1
Number
of ways of filling-up first, second, — n th place
= n (n-1) (n-2) —— 2.1.
nPn = n!
Concept.
We have nPr = n!/n-r
Putting r = n, we have :-
nPr = n! / (n-r)
But nPn = n!
Clearly it is possible, only when n! = 1
Hence it is proof that 0! = 1
Note : Factorial of negative-number is not defined. The expression –3! has no meaning.
Examples
Q. How many different signals can be made by 5 flags from 8-flags of different colours?
Ans. Number of ways taking 5 flags out of 8-flage = 8P5
= 8!/(8-5)!
= 8 x 7 x 6 x 5 x 4 = 6720
Q. How many words can be made by using the letters of the word “SIMPLETON” taken all at a time?
Ans. There are ‘9’ different letters of the word “SIMPLETON”
Number of Permutations taking all the letters at a time = 9P9
= 9! = 362880.
Number of permutations of n-thing, taken all at a time, in which ‘P’ are of one type, ‘g’ of them are of second-type, ‘r’ of them are of third-type, and rest are all different is given by :-
n!/p! x q! x r!
Example: In how many ways can the letters of the word “Pre-University” be arranged?
13!/2! X 2! X 2!
Number of permutations of n-things, taken ‘r’ at a time when each thing can be repeated r-times is given by = nr.
Proof.
Number of ways of filling-up first –place = n
Since repetition is allowed, so
Number of ways of filling-up second-place = n
Number of ways of filling-up third-place
Number of ways of filling-up r-th place = n
Hence total number of ways in which first, second —-r th, places can be filled-up
= n x n x n ————- r factors.
= nr
Example: A child has 3 pocket and 4 coins. In how many ways can he put the coins in his pocket.
Ans. First coin can be put in 3 ways, similarly second, third and forth coins also can be put in 3 ways.
So total number of ways = 3 x 3 x 3 x 3 = 34 = 81
