Random Experiment
An experiment is said to be a random experiment, if it’s out-come can’t be predicted with certainty.
Example
If a coin is tossed, we can’t say, whether head or tail will appear. So it is a random experiment.Sample Space
The set of all possible out-comes of an experiment is called the sample space. It is denoted by ‘S’ and its number of elements are n(s).
Example
In throwing a dice, the number that appears at top is any one of 1,2,3,4,5,6. So here:S ={1,2,3,4,5,6} and n(s) = 6
Similarly in the case of a coin, S={Head,Tail} or {H,T} and n(s)=2.
Elements
The elements of the sample space are called sample point or event point.
Event
Every subset of a sample space is an event. It is denoted by ‘E’.
Example
In throwing a dice S={1,2,3,4,5,6}, the appearance of an event number will be the event E={2,4,6}.Clearly E is a sub set of S.
Simple event
An event, consisting of a single sample point is called a simple event.
Example
In throwing a dice, S={1,2,3,4,5,6}, so each of {1},{2},{3},{4},{5} and {6} are simple events.Compound event
A subset of the sample space, which has more than on element is called a mixed event.
Example
In throwing a dice, the event of appearing of odd numbers is a compound event, because E={1,3,5} which has ‘3’ elements.Equally likely events
Events are said to be equally likely, if we have no reason to believe that one is more likely to occur than the other.
Example
When a dice is thrown, all the six faces {1,2,3,4,5,6} are equally likely to come up.Exhaustive events
When every possible out come of an experiment is considered.
Example
A dice is thrown, cases 1,2,3,4,5,6 form an exhaustive set of events.Classical definition of probability:
If ‘S’ be the sample space, then the probability of occurrence of an event ‘E’ is defined as:
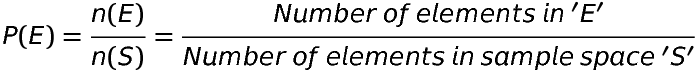
Example
Find the probability of getting a tail in tossing of a coin.Solution
Sample space S = {H,T} and n(s) = 2
Event ‘E’ = {T} and n(E) = 1
therefore 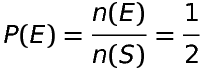
Note: This definition is not true, if
(a) The events are not equally likely.
(b) The possible outcomes are infinite.
Sure event
Let ‘S’ be a sample space. If E is a subset of or equal to S then E is called a sure event.
Example
In a throw of a dice, S={1,2,3,4,5,6}Let E1=Event of getting a number less than ‘7’.
So ‘E1‘ is a sure event.
So, we can say, in a sure event n(E) = n(S)
Mutually exclusive or disjoint event
If two or more events can’t occur simultaneously, that is no two of them can occur together.
Example
When a coin is tossed, the event of occurrence of a head and the event of occurrence of a tail are mutually exclusive events.Pictorial Representation:

Independent or mutually independent events
Two or more events are said to be independent if occurrence or non-occurrence of any of them does not affect the probability of occurrence or non-occurrence of the other event.
Example
When a coin is tossed twice, the event of occurrence of head in the first throw and the event of occurrence of head in the second throw are independent events.Difference between mutually exclusive an mutually independent events
Mutually exclusiveness id used when the events are taken from the same experiment, where as independence is used when the events are taken from different experiments.
Complement of an event
Let ‘S’ be the sample for random experiment, and ‘E’ be an event, then complement of ‘E’ is is denoted by E1. Here E occurs, if and only if E1 doesn’t occur.
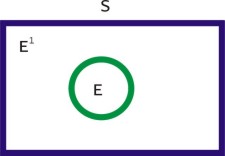
Clearly 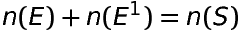
Random Experiment
An experiment is said to be a random experiment, if its out-come can’t be predicted with certainly.
Example
If a coin is tossed, we can’t say, whether head or rail will appear. So it is a random experiment.Sample Space
The set of all possible out-comes of an experiment is called the sample – space.
If a dice is thrown, the number, that appears at top is any one of 1, 2, 3, 4, 5, 6,
So here :
S = { 1, 2, 3, 4, 5, 6, } and n(s) = 6
Similarly in the case of a coin, s = {H,T} and n (s) = 2.
The elements of the sample of the sample-space are called sample points or event points.
Example
if S = {H, T}, than ‘H’ and ‘T’ are sample points.Event: Every subset of a sample space is an event. It is denoted by ‘E’.
Example
In throwing a dice S = {1, 2, 3, 4, 5, 6,}, the appearance of an even number will be the event E = {2, 4, 6}.Clearly 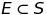
Important types of Events
Simple or elementary event
An event, consisting of a single point is called a simple event.
Example
In throwing a dice s = {1, 2, 3, 4, 5, 6} so each of {1}, {2}, {3}, {4}, {5} and {6} is a simple event.Compound or mixed event
A subset of the sample space which has more than one element is called a mixed event.
Example
In throwing a dice, the event of odd numbers appearing is a mixed event, because E = {1, 3, 5}, which has ‘3’ elements.Equally likely events
Events are said to be equally likely, if we have no reason to believe that one is more likely to occur than the other.
Example
When a dice is thrown, all the six-faces {1, 2, 3, 4, 5, 6,} are equally likely to come-up.Exhaustive events
When every possible outcome of an experiment is considered, the observation is called exhaustive events.
Example
When a dice is thrown, cases 1, 2, 3, 4, 5, 5 form an exhaustive set of events.Algebra of Events
In a random experiment, let ‘S’ be the sample – space.
Let A  S and B
S and B ![]() S,
where ‘A’ and ‘B’ are events.
S,
where ‘A’ and ‘B’ are events.
Thus we say that :
(i)
(A B), is
an event occurs only when at least of ‘A’
and ‘B’ occurs.
B), is
an event occurs only when at least of ‘A’
and ‘B’ occurs. ![]() (A
(A ![]() B) means (A or
B).
B) means (A or
B).
Example
if A = { 2,4,6,} and B = {1, 6}, than the event ‘A’ or ‘B’ occurs, if ‘A’ or ‘B’ or both occur i.e. at least one of ‘A’ and ‘B’ occurs. Clearly ‘A’ or ‘B’ occur, if the out come is any one of the outcomes 1, 2, 4, 6. That is A
(ii)
(A ![]() B)
is an event, that occurs only when each one of
‘A’ and ‘B’ occur
B)
is an event, that occurs only when each one of
‘A’ and ‘B’ occur  (A
(A ![]() B)
means ( A and B).
B)
means ( A and B).
Example
In the above example, if the out come of an experiment is ‘6’, then events ‘A’ and ‘B’ both occur, because ‘6’ is in both sets. That is A
(iii)
A is an event, that occurs only when ‘A’
doesn’t occur.
Categories of Problems Related to Probability
Category A
When n(E) and n(S) are determined by writing down the elements of ‘E’ and ‘S’.Category B
When n(E) and n(S) are calculated by the use of concept of permutation and combination.Category C
Problems based on P(E) + P(E1) = 1Category A: When n(E) and n(S) are determined by writing down the elements of ‘E’ and ‘S’
Question
A coin is tossed successively three times. Find the probability of getting exactly one head or two heads.Solution
Let ‘S’ be the sample – space. Then, S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}Let ‘E’ be the event of getting exactly one head or two heads. Then: E = { HHT, HTH, THH, TTH, THT, HTT }
Question
Three coins are tossed. What is the probability of getting (i) all heads, (ii) two heads, (iii) at least one head, (iv) at least two heads?
Solution
Let ‘S’ be the sample – space. ThenS = { HHH, HHT, HTH, THH, HTT, THT, TTH, TTT }
(i)
Let ‘E1‘ = Event of getting all
heads.
Then E1 = { HHH }
n (E1) = 1
![]() P(E1)
= n (E1) / n(S)
= 1 / 8
P(E1)
= n (E1) / n(S)
= 1 / 8
(ii)
Let E2 = Event of getting
‘2’ heads.
Then:
E2 = { HHT, HTH, THH }
n(E2) = 3
![]() P (E2)
= 3 / 8
P (E2)
= 3 / 8
(iii)
Let E3 = Event of getting at least one
head.
Then:
E3 = { HHH, HHT, HTH, THH, HTT, THT, TTH }
n(E3) = 7
![]() P (E3) = 7
/ 8
P (E3) = 7
/ 8
(iv)
Let E4 = Event of getting at least one
head.
Then:
E4 = { HHH, HHT, HTH, THH, }
n(E4) = 4
![]() P (E4) =
4/8
= 1/2
P (E4) =
4/8
= 1/2
Question
What is the probability, that a number selected from 1, 2, 3, — 2, 5, is a prime number, when each of the numbers is equally likely to be selected.
Solution
S = { 1, 2, 3, —- , 2, 5} >
And E
= { 2, 3, 5, 7, 11, 13, 17, 19, 23 } ![]() n(E)
= 9
n(E)
= 9
Hence P(E) = n(E) / n(S) = 9 / 25
Question
Two dice are thrown simultaneously. Find the probability of getting : (i) The same number on both dice, (ii) An even number as the sum, (iii) A prime number as the sum, (iv) A multiple of ‘3’ as the sum, (v) A total of at least 0, (vi) A doublet of even numbers, (vii) A multiple of ‘2’ on one dice and a multiple of ‘3’ on the other dice.Solution
Here:S = { (1,1), (1,2) ——, (1,6), (2,1), (2,2), —- (2,6), (3,1), (3,2), —–, (3,6), (4,1), (4,2), ——– (4,6), (5,1), (5,2), —– (5,6), (6,1,), (6,2), ————— (6,6) }
n(S) = 6 x 6 = 36(i) Let E1 = Event of getting same number on both side:
(ii) Let E2 = Event of getting an even number as the sum. E2 = { (1,1), (1,3), (1,5), (2,2), (2,4), (2,6), (3,1), (3,3), (3,5), (4,2), (4,4),
(4,6), (5,1), (5,5), (6,2), (6,4), (6,6) }
n(E2) = 18 hence P(E2) = n(E2)/n(S) = 18/36 = 1/2(iii) Let E3 = Event of getting a prime number as the sum.. E3 = { (1,1), (1,2), (1,4), (1,6), (2,1), (2,3), (2,5), (3,2), (3,4), (4,1), (4,3),
(5,2), (5,6), (6,1), (6,5),}
n(E3) = 15 P(E2) = n(E3) / n(S) = 15/36 = 5/12(iv) Let E4 = Event of getting a multiple of ‘3’ as the sum. E4 = { (1,2), (1,5), (2,1), (2,4), (3,3), (3,6), (4,2), (4,5), (5,1), (5,4), (6,3), (6,6),} n(E4) = 12 P(E4) = n(E4)/n(S) = 12/36 = 1/3
(v) Let E5 = Event of getting a total of at least 10. E5 = { (4,6), (5,5), (5,6), (6,4), (6,5), (6,6), } n(E5) = 6 P(E5) = n(E5)/n(S) = 6/36 = 1/6
(vi) Let E6 = Event of getting a doublet of even numbers. E6 = { (2,2), (4,4), (6,6), } n(E6) = 3 P(E6) = n(E6)/ n(S) = 3/36 = 1/12
(vii) Let E7 = Even of getting a multiple of ‘2” on one dice and a multiple of ‘3’ on the other dice.
E7 = { (2,3), (2,6), (4,3), (4,6), (6,3), (3,2), (3,4), (3,6), (6,2), (6,4) } n(E7) = 11 P(E7) = n(E7) / n(S) = 11/36Question
What is the probability, that a leap year selected at random will contain 53 Sundays?Solution
A leap year has 366 days, therefore 52 weeks i.e. 52 Sunday and 2 days.The remaining 2 days may be any of the following :
(i) Sunday and Monday
(ii) Monday and Tuesday
(iii) Tuesday and Wednesday
(iv) Wednesday and Thursday
(v) Thursday and Friday
(vi) Friday and Saturday
(vii) Saturday and Sunday
For having 53 Sundays in a year, one of the remaining 2 days must be a Sunday.
n(S) = 7
n(E) = 2
P(E) = n(E) / n(S) = 2 / 7
Category B: Problems based on fundamental principal of counting and permutations and combinations
Question
A bag contains ‘6’ red, 4 white and 8 blue balls. If three balls are drawn at random, find the probability, that(i) ‘1’ is red and ‘2’ are white, (ii) ‘2’ are blue and 1 is red, (iii) none is red.
Solution
We have to select ‘3’ balls, from 18 balls (6+4+8)
![]() n(S) = 18C3 = 18! / (3!
x 15!) = (18x17x16) / (3x2x1) = 816
n(S) = 18C3 = 18! / (3!
x 15!) = (18x17x16) / (3x2x1) = 816
(i)
Let E1 = Event of getting ‘1’ ball
is red and ‘2’ are white
Total number of ways = n(E1) = 6C1 x 4C2
= 6! / (1! x 5!) x 4! / (2! x 2!)
= 6 x 4 / 2
= 36
P (E1) = n (E1) / n(S) = 36/816 = 3/68
(ii)
Let E2 = Event of getting ‘2’ balls
are blue and ‘1’ is red.
= Total no. of ways ![]() n(E2) = 8C2
x 6C1
n(E2) = 8C2
x 6C1
= 8! / (2! x 6!) x 6! / (1! x 5!)
= (8 x 7) / 2 x 6 / 1 = 168
P(E2) = 168 / 816 = 7/34
(iii)
Let E3 = Event of getting ‘3’
non – red balls. So now we have to choose all the
three balls from 4 white and 8 blue balls.
Total number of ways :
n(E3) = 12C3 = 12! / (3! x 9!) = (12x11x10) / (3x2x1) = 220
P(E3) = n(E3) / n(S) = 220 / 816 = 55/204
Question
A box contains 12 bulbs of which ‘4’ are defective. All bulbs took alike. Three bulbs are drawn randomly.What is the probability that :
(i) all the ‘3’ bulbs are defective?
(ii) At least ‘2’ of the bulbs chosen are defective?
(iii) At most ‘2’ of the bulbs chosen are defective?
Solution
We have to select ‘3’ bulbs from 12 bulbs.
![]() n(S) = 12C3
= 12! / (3! x 9!) = (12x11x10) /
(3x2x1) = 220
n(S) = 12C3
= 12! / (3! x 9!) = (12x11x10) /
(3x2x1) = 220
(i)
Let E1 = All the ‘3’
bulbs are defective.
![]() All bulbs have been chosen, from
‘4’ defective bulbs.
All bulbs have been chosen, from
‘4’ defective bulbs.
![]() n(E1) = 4C3
= 4! / (3! x 1!) = 4
n(E1) = 4C3
= 4! / (3! x 1!) = 4
![]() P(E1) = n(E1) /
n(S) = 4 /220 = 1/55
P(E1) = n(E1) /
n(S) = 4 /220 = 1/55
(ii)
Let E2 = Event drawing at least 2
defective bulbs. So here, we can get ‘2’
defective and 1 non-defective bulbs or 3 defective bulbs.
n(E2) = 4C2 x 8C1 + 4C3 [Non-defective bulbs = 8]
= 4! / (2! x 2!) x 8! / (1! x 7!) + 4! / (3! x 1!)
= 4×3 / 2 x 8/1 + 4/1 = 48+4
n(E2) = 52
![]() P(E2) = n(E2) / n(S) =
52/220 = 13/55
P(E2) = n(E2) / n(S) =
52/220 = 13/55
(iii)
Let E3 = Event of drawing at most
‘2’ defective bulbs. So here, we can get no
defective bulbs or 1 is defective and ‘2’ is
non-defective or ‘2’ defective bulbs.
n(E3) = 8C3 + 4C1 x 8C2 + 4C2 x 8C1
= 8? / (3? x 5?) + 4? / (1? x 3?) x 8? / (2? x 6?) + 4? / (2? x 2?) x 8? / (1? x 7?)
= (8x7x6) / (3x2x1) + 4 x (8×7)/2 + (4 x 3) / 2 + 8/1
= 216
P(E3) = n(E3) / n(S) = 216 / 220 = 54 / 55
Question
In a lottery of 50 tickets numbered from ‘1’ to ’50’ two tickets are drawn simultaneously. Find the probability that:(i) Both the tickets drawn have prime number on them,
(ii) None of the tickets drawn have a prime number on it.
Solution
We want to select ‘2’ tickets from 50 tickets.
![]() n(S) = 50C2 = 50? / (2?
x 48?) = (50×49) / 2 = 1225
n(S) = 50C2 = 50? / (2?
x 48?) = (50×49) / 2 = 1225
(i)
Let E1 = Event that both the tickets have
prime numbers Prime numbers between ‘1’ to
’50’ are :
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47.
Total Numbers = 15.
We have to select ‘2’ numbers from these 15 numbers.
![]() n(E1) = 15C2
= 15? / (2? x 13?) = (15×47) / 2 = 105
n(E1) = 15C2
= 15? / (2? x 13?) = (15×47) / 2 = 105
![]() P(E1) = n(E1) / n(S) =
105/1225 = 21/245
P(E1) = n(E1) / n(S) =
105/1225 = 21/245
(ii)
Non prime numbers between ‘1’ to ’50’
= 50-15 = 35
Let E2 = Event that both the tickets have non-prime numbers.
Now we have to select ‘2’ numbers, from ’35’ numbers.
![]() n(E2) = 35C2
= 35? / (2? x 33?) = (35×34) / 2 = 595
n(E2) = 35C2
= 35? / (2? x 33?) = (35×34) / 2 = 595
![]() P(E2) = n(E2) / n(S) =
595 / 1225 = 17/35
P(E2) = n(E2) / n(S) =
595 / 1225 = 17/35
Question
A bag contains 30 tickets, numbered from ‘1’ to ’30’. Five tickets are drawn at random and arranged in ascending order. Find the probability that the third number is 20.
Solution
Total number of ways of selecting ‘5’ tickets from 30 tickets = 30C5
![]() n(S) = 30C5 = 30? /
(5? x 25?) = (30 x 29 x 28 x 27 x 26) / (5 x 4 x 3 x 2 x
1)
n(S) = 30C5 = 30? /
(5? x 25?) = (30 x 29 x 28 x 27 x 26) / (5 x 4 x 3 x 2 x
1)
n(S) = 29 x 27 x 26 x 7
Suppose the ‘5’ tickets are a1, a2,20, a4, a5
They are arranged in ascending order.
![]() a1, a2
a1, a2 ![]() {1, 2, 3, ——- , 19} and a4,
a5
{1, 2, 3, ——- , 19} and a4,
a5 ![]() { 21, 22, 23, —–, 30}
{ 21, 22, 23, —–, 30}
We have to select ‘2’ tickets from first ’19’ tickets and ‘2’ tickets from last 10 tickets.
![]() n(E) = 19C2
x 10C2
n(E) = 19C2
x 10C2
= 19? / (2? x 17?) = 10? / (2? x 8?) = (19 x 18) / 2 = (10 x 9) / 2
= 19 x 9 x 5 x 9
![]() P(E) = n(E) / n(S) = (19x9x5x9) /
(29x27x26x7) = 285 / 5278
P(E) = n(E) / n(S) = (19x9x5x9) /
(29x27x26x7) = 285 / 5278
Odds in Favour and Odds against an Event:
Let ‘S’; be the sample space and ‘E’ be an event. Let ‘E’ devotes the complement of event ‘E’, then.
(i)
Odds in favour of event ‘E’ = n(E) / n(E1)
(ii)
Odds in against of an event ‘E’ = n(E1)
/ n(E)
Note : Odds in favour of ‘E’ = n(E) / n(E1)
= [n(E) / n(S)] / [n(E1) / n(S)] = P(E) / P(E1)
Similarly odds in against of ‘E’ = P(E1) / P(E)
Example
The odds in favours of an event are 3:5 find the probability of the occurrence of this event.
Solution
Let ‘E’ be an event.Then odds in favour of E = n(E) / n(E1) = 3 / 5
![]() n(E) = 3 and n(E1) = 5
n(E) = 3 and n(E1) = 5
Total number of out-comes n(S) = n(E) + n(E1) = 3+5 = 8
P(E) = n(E) / n(S) = 3 / 8
Question
If ’12’ persons are seated at a round table, what is the probability that two particulars persons sit together?
Solution
We have to arrange 12 persons along a round table.So if ‘S” be the sample – space, then n(S) = (12-1)? = 11?
n(S) = 11?
Now we have to arrange the persons in away, such that ‘2’ particulars person sit together.
Regarding that 2 persons as one person, we have to arrange 11 persons.
Total no. of ways = (11-1)? = 10? ways.
That ‘2’ persons can be arranged among themselves in 2? ways.
So, total no. of ways, of arranging 12 persons, along a round table, so that two particular person sit together : = 10? x 2?
![]() n(E) = 10? x 2?
n(E) = 10? x 2?
![]() P(E) = n(E) / n(S) = (10? x 2?) / 11? = 2 /
11
P(E) = n(E) / n(S) = (10? x 2?) / 11? = 2 /
11
Question
6 boys and 6 girls sit in a row randomly, find the probability that all the ‘6’ girls sit together.
Solution
We have to arrange ‘6’ boys and ‘6’ girls in a row.
![]() n(S) = 12?
n(S) = 12?
Now, we have to arrange ‘6’ girls in a way, such that all of them should sit together.
Regarding all the 6 girls as one person, we have to arrange 7 person in a row.
![]() Total no. of ways = 7?
Total no. of ways = 7?
But 6 girls can be arranged among themselves in 6? ways.
![]() n(E) = 7? x 6?
n(E) = 7? x 6?
![]() P(E) = n(E) / n(S) = (7? x 6?) / 12? =
(6x5x4x3x2x1) / (12x11x10x9x8)
P(E) = n(E) / n(S) = (7? x 6?) / 12? =
(6x5x4x3x2x1) / (12x11x10x9x8)
P(E) = 1 / 132
Question
If from a pack of ’52’ playing cards one card is drawn at random, what is the probability that it is either a kind or a queen?Solution
n(S) = Total number of ways of selecting 1 card out of 52 cards.= 52C1 = 52
n(E) = Total number of selections of a card, which is either a kind or a queen.
= 4C1 + 4C1 = 4 + 4 = 8
P(E) = n(E) / n(S) = 8 / 52 = 2 / 3
Question
From a pack of 52 playing cards, three cards are drawn at random. Find the probability of drawing a king, a queen and a jack.
Solution
Here n(S) = 52C3 = 52? / (3? x 49?) = (52x51x50) / (3x2x1)= 52x17x25
n(E) = 4C1. 4C1. 4C1
= 4? / (1? x 3?) x 4? / (1? x 3?) = 4? / (1? x 3?)
n(E) = 4 x 4 x 4
![]() P(E) = n(E) / n(S) = (4x4x4) /
(52x17x25) = 16 / 5525
P(E) = n(E) / n(S) = (4x4x4) /
(52x17x25) = 16 / 5525
Category C:Problems based on finding P(E1), by the use of P(E) + P(E1) = 1
Note : When an event has a lot of out comes, then we use this concept.
Question
What is the probability of getting a total of less than ’12’ in the throw of two dice?Solution
Here n(S) = 6x6x = 36It is very difficult to find out all the cares, in which we can find the total less then ’12’.
So let E = The event, that the sum of numbers is ’12’.
Then E = { 6, 6}
n(E) = 1
![]() P(E) = n(E) / n(S) = 1/36
P(E) = n(E) / n(S) = 1/36
Required probability, P(E1) = 1-P(E)
= 1 – 1/36
P(E1) = 35 /36
Question
There are ‘4’ envelopes corresponding to ‘4’ letters. If the letters are placed in the envelopes at random, what is the probability that all the letters are not placed in the right envelopes?
Solution
We have to place ‘4’ letters in 4 envelopes.
![]() n(S) = 4!
n(S) = 4!
Now:
Let E = The event, that all the 4 letters are placed in the corresponding envelopes.
So E1 = The event that all the ‘4’ letters are not placed in the right envelope.
Here n(E) = 1
P(E) = n(E) / n(S) = 1 / 4! = 1 / 24
Required probability, P(E1) = 1- P(E)
= 1 – (1/24)
P(E1) = 23 / 24
Total Probability
Theorem – 1
If ‘A’ and ‘B’ are mutually exclusive events then P(A
Proof
If ‘A’ and ‘B’ are mutually exclusive events then A B =
B = 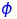
![]() P(A
P(A![]() B) = P(
B) = P(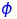 )
)
= n(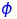 ) / n(S) [ By definition of
probability]
) / n(S) [ By definition of
probability]

= 0 / n(S) [Since the number of elements in a null – set is ‘0’]
P(A![]() B) = 0
B) = 0
Addition Theorem of Probability
If ‘A’ and ‘B’ by any two events, then the probability of occurrence of at least one of the events ‘A’ and ‘B’ is given by:
P(A or B) = P(A) + P(B) – P (A and B)
P(A![]() B) = P(A) + P(B) – P (A
B) = P(A) + P(B) – P (A![]() B)
B)
From set theory, we have :
n(A![]() B) = n(A) + n(B) – n(A
B) = n(A) + n(B) – n(A![]() B)
B)
Dividing both sides by n(S) :
n(A![]() B) / n(S) = n(A) / n(S)
+ n(B) / n(S) – n(A
B) / n(S) = n(A) / n(S)
+ n(B) / n(S) – n(A![]() B) /
n(S)
B) /
n(S)
or P(A![]() B) = p(A) + P(B) – P(A
B) = p(A) + P(B) – P(A![]() B)
B)
Corollary : If ‘A’ and ‘B’ are mutually exclusive events,
Then P(A![]() B) = 0. [ As we have proved]
B) = 0. [ As we have proved]
In this case :
![]() P(A
P(A![]() B) = p(A) + P(B)
B) = p(A) + P(B)
Addition theorem for ‘3’ events ‘A’, ‘B’ and ‘C’
P(A![]() B
B![]() C) = P(A) + P(B) – P(A
C) = P(A) + P(B) – P(A![]() B)
– P(B
B)
– P(B![]() C) – P(A
C) – P(A![]() C) + P(A
C) + P(A![]() B
B![]() C)
C)
Proof
P(A
= P(A![]() b) + P(C) – P[(A
b) + P(C) – P[(A![]() B)
B) ![]() C]
[ By addition theorem for two events]
C]
[ By addition theorem for two events]
= P(A![]() B) – P(C) – [P(A
B) – P(C) – [P(A![]() C) +
P(B
C) +
P(B![]() C)
– P(A
C)
– P(A![]() C
C![]() B
B![]() C)]
C)]
= P(A) + P(B) – P(A![]() B) +
P(C) – P(A
B) +
P(C) – P(A![]() C) – P(B
C) – P(B![]() C) + P(A
C) + P(A![]() B
B![]() C)
C)
P(A![]() B
B![]() C) = P(A) + P(B) + P(C) – P(A
C) = P(A) + P(B) + P(C) – P(A![]() B)
– P(B
B)
– P(B![]() C) – P(A
C) – P(A![]() C) + P(A
C) + P(A![]() B
B![]() C)
C)
Corollary : If ‘A’,
‘B’ and ‘C’ are mutually exclusive
events, then P(A![]() B) = 0, P(B
B) = 0, P(B![]() C) = 0,
P(A
C) = 0,
P(A![]() C)
= 0 and P(A
C)
= 0 and P(A![]() B
B![]() C) = 0.
C) = 0.
In this case :
![]() P(A
P(A![]() B
B![]() C) = P(A) + P(B) + P(C)
C) = P(A) + P(B) + P(C)
General Form of Addition Theorem of Probability
n
P(A1 ![]() A2
A2 ![]() —–
—– ![]() An)
=
An)
= ![]() P(Ai) –
P(Ai) – ![]() P(Ai
P(Ai
![]() Aj)
Aj)
i=1 i<j
+ ![]() P(Ai
P(Ai ![]() Aj
Aj
![]() Ak)
—– (-1)n-1 P(A1
Ak)
—– (-1)n-1 P(A1 ![]() A2
A2
![]() —-
—- ![]() An)
An)
i<j<k
Corollary : For any number of mutually exclusive events, A1, A2, —— , An :
P(A1 ![]() A2
A2 ![]() —-
—- ![]() An)
= P(A1) + P(A2) + —— +
P(An)
An)
= P(A1) + P(A2) + —— +
P(An)
Theorem – 3 : For any two events ‘A’ and ‘B’
P(A-B) = P(A) – P(A B) =
P(A
B) =
P(A![]() B1)
B1)

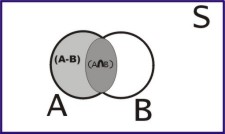
From the figure:
(A-B) ![]() (A
(A![]() B) =
B) = 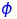 —————> (i)
—————> (i)
and
(A-B) ![]() (A
(A![]() B) = A
B) = A
P[(A-B) ![]() (A
(A![]() B)] = P(A)
B)] = P(A)
or P(A-B) + P(A![]() B) =
P(A)
B) =
P(A)
[From (i) (A-B)![]() (A
(A![]() B)
=
B)
= 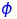 i.e. These events are mutually exclusive]
i.e. These events are mutually exclusive]
![]() P(A-B) = P(A) – P(A
P(A-B) = P(A) – P(A![]() B)
B)
or P(A![]() B) = P(A) – P(A
B) = P(A) – P(A![]() B)
B)
Similarly P(A![]() B) =
P(B) – P(A
B) =
P(B) – P(A![]() B)
B)
Proof of P(E) + P(E1) = 1, by the addition theorem of probability:
We know that :
P(A ![]() B) = P(A) + P(B) – P(A
B) = P(A) + P(B) – P(A![]() B)
B)
Putting A = E and B = E1
P (E ![]() E1) = P(E) + P(E1)
– P (E
E1) = P(E) + P(E1)
– P (E![]() E1) —————-> (1)
E1) —————-> (1)
From set theory : E
![]() > E1
= S
> E1
= S
And E ![]() E1 =
E1 = 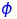
From:
P(S) = P(E) + P(E1) – P(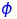 )
)
![]() 1 = P(E) + P(E1)
– 0
1 = P(E) + P(E1)
– 0
or P(E) + P(E1) = 1
[P(S) = 1, P(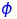 ) = 0]
) = 0]
EXAMPLES
Problems based on addition theorem of probability
Working rule :
(i)
A ![]() B
denotes the event of occurrence of at least one of the
event ‘A’ or ‘B’
B
denotes the event of occurrence of at least one of the
event ‘A’ or ‘B’
(ii)
A ![]() B denotes the event of occurrence of both the events
‘A’ and ‘B’.
B denotes the event of occurrence of both the events
‘A’ and ‘B’.
(iii)
P(A![]() B) or
P(A+B) denotes the probability of occurrence of at least
one of the event ‘A’ or ‘B’.
B) or
P(A+B) denotes the probability of occurrence of at least
one of the event ‘A’ or ‘B’.
(iv)
P(![]() B)
or P(AB) denotes the probability of occurrence of both
the event ‘A’ and ‘B’.
B)
or P(AB) denotes the probability of occurrence of both
the event ‘A’ and ‘B’.
Question
The probability that a contractor will get a contract is ‘2/3’ and the probability that he will get on other contract is 5/9 . If the probability of getting at least one contract is 4/5, what is the probability that he will get both the contracts ?
Solution
Here P(A) = 2/3, P(B) = 5/9
P(A![]() b) = 4/5, (P(A
b) = 4/5, (P(A![]() B) = ?
B) = ?
By addition theorem of Probability:
P(A![]() B) = P(A) + P(B) – P(A
B) = P(A) + P(B) – P(A![]() B)
B)
= 4/5 = 2/3 + 5/9
– P(A![]() B)
B)
or 4/5 = 11/9 – P(A![]() B)
B)
or P(A![]() B) = 11/9 – 4/5
= (55-36) / 45
B) = 11/9 – 4/5
= (55-36) / 45
P(A![]() B) = 19/45
B) = 19/45
Question
Two cards are drawn at random. Find the probability that both the cards are of red colour or they are queen.
Solution
Let S = Sample – space.A = The event that the two cards drawn are red.
B = The event that the two cards drawn are queen.
![]() A
A![]() B = The event that the two cards drawn are
queen of red colour.
B = The event that the two cards drawn are
queen of red colour.
![]() n(S) = 52C2,
n(A) = 26C2, n(B) = 4C2
n(S) = 52C2,
n(A) = 26C2, n(B) = 4C2
n(A![]() B) = 2C2
B) = 2C2
![]() P(A) = n(A) / n(S) = 26C2
/ 52C2 , P(B) = n(B) /
n(S) = 4C2 / 52C2
P(A) = n(A) / n(S) = 26C2
/ 52C2 , P(B) = n(B) /
n(S) = 4C2 / 52C2
P(A![]() B) = n(A
B) = n(A![]() B) /
n(S) = 2C2 / 52C2
B) /
n(S) = 2C2 / 52C2
P(A![]() B) = ?
B) = ?
We have P(A![]() B) = P(A) + P(B) – P(A
B) = P(A) + P(B) – P(A![]() B)
B)
= 26C2 / 52C2 + 4C2 / 52C2 – 2C2 / 52C2
= (26C2 + 4C2 – 2C2) / 52C2
= (13X25+2X3-1) / (26X51)
P(A![]() B) = 55/221
B) = 55/221
Question
A bag contains ‘6’ white and ‘4’ red balls. Two balls are drawn at random. What is the chance, they will be of the same colour?
Solution
Let S = Sample spaceA = the event of drawing ‘2’ white balls.
B = the event of drawing ‘2’ red balls.
A![]() B = The
event of drawing 2 white balls or 2 red balls.
B = The
event of drawing 2 white balls or 2 red balls.
i.e. the event of drawing ‘2’ balls of same colour.
![]() n(S) = 10C2 = 10!
/ (2! x 8!) = 45
n(S) = 10C2 = 10!
/ (2! x 8!) = 45
n(A) = 6C2 = 6! / ((2! x 4!) = (6 x 5 ) / 2 = 15
n(B) = 4C2 = 4! / (2! x 2!) = (4×3) / 2 = 6
P(A) = n(A) / n(S) = 15/45 = 1/3
P(B) = n(B) / n(S) = 6/45 = 2/15
![]() P(A
P(A![]() B) = P(A) + P(B)
B) = P(A) + P(B)
= 1/3 + 2/15 = (5+2) / 15
P(A![]() B) = 7/15
B) = 7/15
Question
For a post three persons ‘A’, ‘B’ and ‘C’ appear in the interview. The probability of ‘A’ being selected is twice that of ‘B’ and the probability of ‘B’ being selected is thrice that of ‘C’, what are the individual probability of A, B, C being selected?
Solution
Let ‘E1‘, ‘E2‘, ‘E3‘ be the events of selections of A, B, and C respectively.Let P(E3) = x
![]() P(E2) = 3. P(E3)
= 3x
P(E2) = 3. P(E3)
= 3x
and P(E1) = 2P(E2) = 2 x 3x = 6x
As there are only ‘3’ candidates ‘A’, ‘B’ and ‘C’ we have to select at least one of the candidates A or B or C, surely.
![]() P( E1
P( E1 ![]() E2
E2 ![]() E3)
= 1
E3)
= 1
and E1, E2, E3 are mutually exclusive.
![]() P(E1
P(E1![]() E2
E2 ![]() E3)
= P(E1) + P(E2) + P(E3)
E3)
= P(E1) + P(E2) + P(E3)
1 = 6x + 3x + x
![]() 10x – 1 or x = 1/10
10x – 1 or x = 1/10
![]() P(E3) = 1/10, P(E2)
= 3/10 and P(E1) = 6/10
= 3/5
P(E3) = 1/10, P(E2)
= 3/10 and P(E1) = 6/10
= 3/5